Học Machine Learning

Các bài học Machine Learning cơ bản

Bài 1: Linear Algebra – Scalar, Vector, và Matrix

by · Published · Updated

Xin chào các bạn, như đã nói ở bài viết trước, mình sẽ bắt đầu chuỗi bài học Machine Learning bằng các kiến thức cơ bản nhất về Đại Số Tuyến Tính (Linear Algebra). Sau đây mình sẽ định nghĩa sơ lược về môn học này, và sẽ giới thiệu cho các bạn về các thành phần cơ bản nhất của Linear Algebra, đó là scalar, vector (véc-tơ) và matrix (ma trận)

Source: What is difference between vector and matrix? | Basic things. (wordpress.com)

Linear Algebra là gì?

Linear Algebra (hay Đại số Tuyến tính) là một nhánh nhỏ của Toán học, tập trung chủ yếu vào các ma trận, véc-tơ, cũng như là các phép tính toán liên quan đến các toán tử này. Các phép tính có thể là phép cộng, trừ, nhân, chia như trong môn Số Học mà chúng ta đã từng được trải nghiệm ở cấp 2 hay cấp 3, nhưng nó cũng bao gồm nhiều ý tưởng phức tạp hơn như là tìm determinant, hay xác định eigenvalues hay eigenvectors của một ma trận nữa (yên tâm nha, mình sẽ đi qua hết mấy phép toán nghe có vẻ xa xăm này). Các bạn chắc hẳn đã từng trải nghiệm một chút về môn học này khi học cấp 2 và cấp 3, khi chúng ta tìm hiểu về các đường thẳng và mặt phẳng trong không gian 2 và 3 chiều (hình như khái niệm vector cũng đã xuất hiện ở thời điểm đó).

Cá nhân mình thì thường hình dung Linear Algebra như là một bước khái quát hóa cùa môn Số Học vậy đó: hồi xưa thì chúng ta thường xem các con số, như 1, 2, 3,... là các cấu phần cơ bản nhất của toán học. Khi học Linear Algebra thì được nâng cấp lên một tí, các cấu phần cơ bản bây giờ sẽ là véc-tơ và ma trận. Vậy thì bước tiếp theo là tìm hiểu về các thành phần này!

Scalar

Như tựa đề, scalar chỉ đơn giản là một con số bất kì, như là 1, 2, 3, \frac{1}{2}, \pi,.. mà ai học cấp 1 rồi cũng biết vậy á. Scalar khi mà được dịch ra tiếng Việt thì là “vô hướng”, cách dịch này theo mình hiểu là để đối lập với sự “có hướng” của vector vậy đó (cái này thì qua phần vector mình sẽ tìm hiểu nha). Scalar có vai trò rất quan trọng trong Linear Algebra, vì nó là cấu phần tạo nên tất cả vector hoặc matrix. Thực tế, vector hay matrix đơn giản chỉ là một danh sách (list) chứa các con số này.

Vector

Vector được định nghĩa là một đại lượng có hướng và có độ lớn, một khái niệm cơ bản mà chúng ta đã được học ở cấp 3. Một ví dụ cụ thể là lực tác động lên một vật thể, lực thì phải có hướng xác định (khi bạn ném một vật theo phương ngang thì lực đó có phương nằm ngang, ném lên trời thì lực theo phương thẳng đứng) và độ lớn xác định (lực càng mạnh thì vật bay càng xa). Tương tự đối với vận tốc cũng vậy. Vì thế nên là lực, hay là vận tốc thường được biểu diễn như là một vector trong không gian 2 hoặc 3 chiều. Và để minh họa cho các đại lượng này thì người ta thường vẽ một mũi tên trong hệ trục tọa độ Oxy và Oxyz.

Biểu diễn lực trong không gian 2 chiều (Oxy). Source: Vectors (smu.edu)

Vector được biểu diễn dưới dạng một danh sách bao gồm các vô hướng (scalar mà chúng ta đã nhắc đến ở trên), ví dụ như vector sau:

x = \begin{bmatrix} 1\\2 \end{bmatrix} và y = \begin{bmatrix} 1\\2\\3 \end{bmatrix}

Kích thước (hay chiều) của một vector thì được xác định bằng cách đếm số lượng vô hướng trong vector đó, trong ví dụ ở trên thì x là vector 2 chiều (2-dimensional vector) và y là vector 3 chiều (3-dimensional vector). Người ta thường kí hiệu chiều của một vector bằng cách viết: x \in \mathbb{R}^{2} và y \in \mathbb{R}^{3}, khái quát hơn là x \in \mathbb{R}^{D} trong đó D là số chiều/kích thước của vector. Cái này giống như là tập hợp các số thực ấy, bạn chỉ cần thêm số mũ (tượng trưng cho số chiều của vector) vào thôi.

Lưu ý nhỏ là có hai “loại” vector mà chúng ta thường gặp, đó là row vector (vector có dạng hàng) và column vector (vector có dạng cột). Cũng dễ hiểu lắm, row vector thì được viết dưới dạng một dãy số nằm ngang, còn column vector thì là một cột số thẳng đứng:

x = \begin{bmatrix} 1 & 2 & 3 \end{bmatrix} là row vector trong khi đó y = \begin{bmatrix} 1\\2\\3 \end{bmatrix} là column vector

Tuy là x và y chứa các con số giống nhau, nhưng mà row vector và column vector không bằng nhau nha, nên là x \ne y

Trong Machine Learning, tồn tại một khái niệm có tên là feature vector, đây là một vector dùng để biểu diễn các tính chất hay đặc điểm của một điểm dữ liệu (data point). Ví dụ như là một ngôi nhà có năm tầng, và có hai phòng khách chẳng hạn, feature vector của ngôi nhà này có thể là:

x_{1} = \begin{bmatrix} 5\\2 \end{bmatrix} trong đó 5 là số tầng và 2 là số phòng khách

Một căn nhà khác có số tầng là 2 và có 4 phòng khách, thì feature vector của nó là:

x_{2} = \begin{bmatrix} 2\\4 \end{bmatrix}

Các feature vector của nhiều điểm dữ liệu khác nhau có thể được gộp chung lại thành một ma trận (gọi là design matrix). Mình sẽ tìm hiểu về matrix ngay sau đây.

Matrix

Nghĩ một cách đơn giản thì ma trận là một “hình chữ nhật” chứa nhiều vô hướng, ví dụ là x = \begin{bmatrix} 1 & 2 & 3\\2 & 3 & 4 \end{bmatrix}. Nếu vector chỉ có thể theo một “hướng”, dọc hoặc ngang thì ma trận có thể có phương dọc và phương ngang luôn. Chiều hay kích thước của một ma trận thì vô hình vạn trạng, có rất là nhiều kích thước khác nhau, như là:

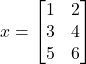x = \begin{bmatrix} 1 & 2 & 3\\4 & 5 & 6 \end{bmatrix} có hai hàng và ba cột, trong khi đó x = \begin{bmatrix} 1 & 2\\3&4\\5&6\end{bmatrix} có ba hàng và hai cột.

Như trong trường hợp row vector và column vector đó, dù chứa các vô hướng giống nhau nhưng mình không thể nói x = y được, do là chúng có kích thước khác nhau. Để biểu hiện cho kích thước cho matrix thì người ta đếm số hàng và số cột, rồi kí hiệu là matrix \in \mathbb{R}^{rows \times columns} trong đó rows là số hàng và columns là số cột. Ở ví dụ trên thì x \in \mathbb{R}^{2\times3} và y \in \mathbb{R}^{3\times2}.

Quay lại với ví dụ trong ML thì có khái niệm là design matrix, tức là một ma trận chứa feature vector của tất cả các điểm dữ liệu. Để minh họa thì tưởng tượng là ta có 3 căn nhà, nhà 1 có 2 tầng, 1 phòng khách, nhà 2 có 3 tầng, 4 phòng khách và nhà 3 có 5 tầng, 5 phòng khách, thì feature vectors của 3 điểm dữ liệu này lần lượt là:

x_1 = \begin{bmatrix} 2\\1\end{bmatrix}, x_2 = \begin{bmatrix} 3\\4\end{bmatrix}, x_3 = \begin{bmatrix} 5\\5\end{bmatrix}

Để tạo ra một design matrix cho các điểm dữ liệu này thì mình chỉ cần gộp chúng lại với nhau, theo phương nằm ngang, tức là:

design matrix = \begin{bmatrix} \rule{1cm}{0.4px}x_1^T\rule{1cm}{0.4px}\\\rule{1cm}{0.4px}x_2^T\rule{1cm}{0.4px}\\\rule{1cm}{0.4px}x_3^T\rule{1cm}{0.4px} \end{bmatrix} = \begin{bmatrix} 2&1\\3&4\\5&5 \end{bmatrix}

Trong đó kí hiệu x_1^T đơn giản chỉ là xoay ngang vector đó lại (transpose operation – mình sẽ học ở các bài tiếp theo), nếu x_1 = \begin{bmatrix} 2\\1\end{bmatrix} thì x_1^T = \begin{bmatrix} 2&1\end{bmatrix} (là row vector đó!). Sau đó thì mình chỉ cần xếp chồng 3 row vector này với nhau để tạo nên một design matrix.

Lưu ý nhỏ là row vector hay column vector có thể xem như là một dạng đặc biệt của matrix, trong đó thì số hàng bằng 1 (đối với row vector) và số cột bằng 1 (đối với column vector), ví dụ là x = \begin{bmatrix} 2 & 1\end{bmatrix} \in \mathbb{R}^{1\times2} hay y = \begin{bmatrix} 2\\1\end{bmatrix} \in \mathbb{R}^{2\times1}.

Tiếp theo

Ở bài viết sau, chúng ta sẽ cùng tìm hiểu về các phép tính trên vector và matrix nha. Mong các bạn đón đọc!

You may also like...

Leave a Reply

Your email address will not be published.